Naive Bayesian Classifier Based On Gaussian Distribution
Section A 一些定理
朴素贝叶斯分类器是一系列以假设特征之间强独立下运用贝叶斯定理为基础的简单分类器 —— 维基百科
贝叶斯定理
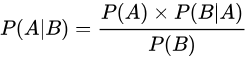
其中P(A|B)是在B发生的情况下A发生的可能性。
- P(A|B)是已知B发生后A的条件概率,也由于得自B的取值而被称作A的后验概率。
- P(A)是A的先验概率(或边缘概率)。之所以称为"先验"是因为它不考虑任何B方面的因素。
- P(B|A)是已知A发生后B的条件概率,也由于得自A的取值而被称作B的后验概率。
- P(B)是B的先验概率或边缘概率。
以上可表述为
后验概率 = (可能性*先验概率)/标准化常量
###高斯朴素贝叶斯
如果要处理的连续数据服从高斯分布(正态分布),那么概率密度可以通过下图公式计算出来
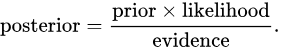
Section B 一些实现代码
(ns naive-bayesian.core
(:require [clojure.core.matrix :as mat]
[clojure.core.matrix.stats :as mats]))
(defn probability-density [x arr]
(let [variance (mats/variance arr)
mean (mats/mean arr)]
(* (/ 1 (Math/sqrt (* 2 Math/PI variance)))
(Math/pow Math/E (/ (- (Math/pow (- x mean) 2)) (* 2 variance)))) ))
(defn gaussian-probability-assumption [r rs]
(reduce *
(map
(fn [x]
(probability-density (x r)
(into-array Double/TYPE (map x rs))))
(map key r))))
在实现方式上面其实并不困难,注意不要写错顺序就可以了。就是简单的套用公式。
解释
probability-density这个函数用来计算上述公式的,gaussian-probability-assumption这个是用来计算在给定了一条记录,一组数据集下面的满足下面公式的函数
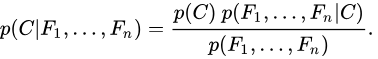
用朴素的语言可以表述为
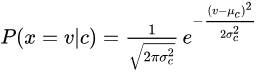
示例
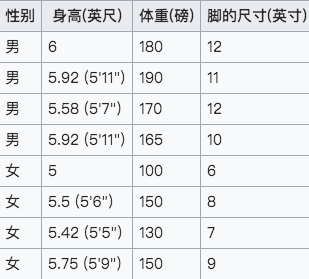
以下给出一个待分类是男性还是女性的样本

我们希望得到的是男性还是女性哪类的后验概率。 以此可以判断满足该组数据的人是男性还是女性。
;;sample test case
; (def r {:a 6 :b 130 :c 8})
; (def rs [
; {:a 6 :b 180 :c 12}
; {:a 5.92 :b 190 :c 11}
; {:a 5.58 :b 170 :c 12}
; {:a 5.92 :b 165 :c 10}
; ])
; (def rs1 [
; {:a 5 :b 100 :c 6}
; {:a 5.5 :b 150 :c 8}
; {:a 5.42 :b 130 :c 7}
; {:a 5.75 :b 150 :c 9}
; ])
; (> (gaussian-probability-assumption r rs)
; (gaussian-probability-assumption r rs1))
思考
在给出一些奇怪条件的情况下,可以得到一个满足这些条件的答案,看似不合常理,但是确实是这个道理。
举个例子,一艘船上有26只绵羊和10只山羊,船上船长几岁?
上述示例其实就是一个类似的问题,一个身高6英尺,体重130磅,脚长8英尺的人是男还是女,乍一看之下是非常莫名其妙的,但是背后所包含的数学问题其实非常简单且精妙,以至于我们似乎忘记了数学其实无处不在。