贝叶斯分类器的先验分布

在获取数据之前，通过共轭先验和无信息先验两种方式，确定先验分布

1. 共轭先验

   事物某个特征的真值（也称参数）具有不确定性，是服从某种概率分布的随机变量θ，可用π(θ)表示随机变量θ的概率函数。

   θ为连续型随机变量时，π(θ)为密度函数。θ为离散型随机变量时，π(θ))为概率。

   利用数据D对θ调整的结果，就是参数\theta的后验分布π(θ)。

   θ为连续型随机变量时，后验分布为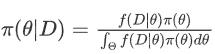，其中Θ称为参数空间

   θ为离散型随机变量时

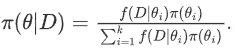
   • 当θ已知而D为随机变量的情况下，f(D|θ)是D的概率密度函数

   • D已知θ为随机变量，f(D|θ)描述的是不同参数θ下D出现的概率，也称参数θ似然函数

2. 无信息先验

   • 依据样本分布原则

     依据样本分布原则，即直接基于数据集计算

   • 熵值最大法原则

     若发送信息的，发送的信息u_k的概率为P(u_k)，且，则熵的数学定义为

     

     熵为非负数。如果Ent(U)=0最小，表示只存在唯一的信息发送方案，即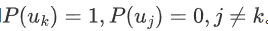。如果信源的k个信息有相同的发送概率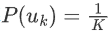，此时信息发送的不确定性最大，熵达到最大.

     信息熵越大，表示平均不确定性越大。反之亦然