预测模型的评价

预测模型的预测精度或预测误差较低时，才能认为模型对新数据的预测会有良好的表现

• 模型误差

  简称误差，是基于数据集，对模型预测值和实际值不一致程序的数据值化度量。

  它包括对每个样本观测的度量和对数据集整体的度量两个部分。

• 预测误差或泛化误差

  是预测模型对新数据集进行预测时，给出的预测值和实际值不一致程度的数值化度量。

  预测误差测试模型在未来新数据集上的预测性能。

• 差别

  预测建模时可直接计算出模型误差的具体值，但因泛化误差聚焦于预测模型未来表现的评价，且建模时未来新数据集是未知的，因此只能给出一个相对客观的估计值

模型误差的评价的指标

• 回归预测模型中的误差评价指标

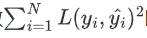  回归预测模型的误差，是输出变量预测值和实际值的差：。数据集.误差程度的整体水平可在总平方损失函数的基础上做适应调整。

  平方损失函数数值受到样本量N的大小的影响，不能直接作为评价指标。

  均方误差（MSE）很好地误差了此影响，其定义为

  
  

  MSE是误差总和的平均值，也是平方损失函数的期望（E表示期望）。其值越大，表示误差越大，反之亦然。

  • 其他模型的评价指标

    • 平均绝对误差

    • 平均绝对误差百分比

• 二分类预测模型中的误差评价指标

  对于分类问题，误差通常基于混淆矩阵计算。混淆矩阵通过矩阵表格形式展示预测类别值与实际类别值的差异程度或一致程度。

  	预测为正样本	预测为负样本
  实际为正样本	True Positive (TP)	False Negative (FN)
  实际为负样本	False Positive (FP)	True Negative (TN)

  基于该混淆矩阵，可派生出若干聚会范围在[0,1]之间的错判率或正确率指标，以度量模型误差或精度

  • 总正确率=

    总正确率越大，越接近1，表明模型的总误差越小，反之亦然

  • 总错判率=

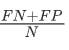
    错判是指模型对输出变量的类别给出了错误判断（预测类别错误）

    总错误率越大，表明模型的总误差越大。

  • 敏感性=

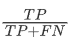
    敏感性是实际类别值等于1的样本中被模型判为1类的比率，记为TPR(True Positive Ratio)

    该值越大，表明模型对1类判断的误差越小，反之亦然

  • 特异性=

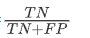
    特异性是实际类别值等于0的样本中模型判为0类的比率，记为TNR(True Negative Ratio)

    同时，1-TNR为假正率，记为FPR(False Positive Ratio)

    TNR越大，表明模型对0类判断的误差越小，反之亦然

  • 查准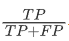率=与查全率=

    查准率（Precision）是被模型判为1类的样本中实际确为1类的比率，记为P

    查全率（Recall）记为R，等价于敏感性，专用于评价信息检索算法的性能

  • F1分数=

    F1分类是查准率P和查全率R的调和平均值。调和平均值也称倒数平均值，其值越大真好。

    计算F1分类时引入了权重β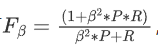，有，有

    β > 1：查准率将对结果有更大影响

    0 < β < 1：评估结果主要取决于查全率

    β = 0：查准率P和查全率R对评估结果有同等权重的影响

• 多分类预测模型中的误差评价指标

  通常多分类预测可间接通过多个二分类预测实现，可采用1对1策略或1对多两种策略

  1对1策略：令第k类为一类，其余类依次作为另一类，分别构建个二分类预测模型

  1对多策略：令第k类为一类，其余k-1个类别都归为另一类，分别构建M=K个二分类预测模型

  无论采种策略都会计算出M个二分类的混淆矩阵，然后依据这些均值计算上述评价指标，由此得到的评价指标统称为微平均(Micro-averaged)意义下的评价指标

模型的图形化评价工具

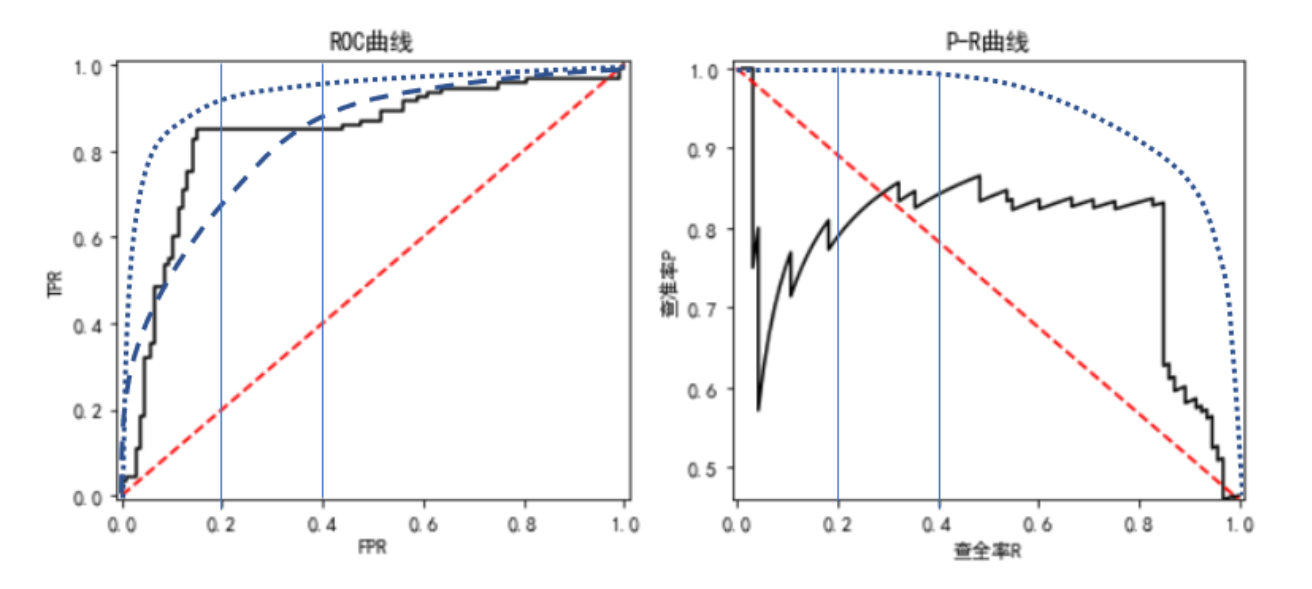
• ROC曲线和AUC值

  ROC曲线的横坐标为FPR，纵坐标为TPR，取值范围是[0,1]区间

• P-R曲线

  P-R曲线是基于查准率P和查全率R绘制的曲线

泛化误差的估计方法

泛化误差是预测模型对新数据集进行预测时，预测值和实际值不一致程度的数值化度量。

1. 训练误差

   用于训练模型的数据集称为训练集(training set)，其中的样本观测称为“袋内观测”。基于训练集“袋内观测”，建立模型并计算得到的模型误差，称为训练误差或经验误差。

   
   

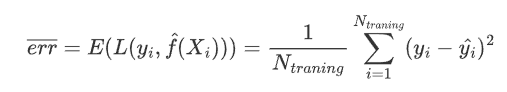
   训练误差的大小与模型复杂度和训练样本量有关。模型复杂度一般可用模型中的待估参数的个数来度量。

   • 一方面，待估参数越多，模型复杂度越高。在恰当的训练样本量条件下，增加模型的复杂度会带来训练误差的降低。原因是高复杂度模型对数据中隐藏规律的刻画更细致，从而使得训练误差减少

   • 另一方面，在模型复杂度确定的条件下，训练误差会随样本量增加而下降。原因是较小规模的训练集无法全面囊括输入变量和输出变量聚会的规律性，建立在其上的预测模型会因不具备“充分学习”的数据条件而导致训练误差较大，随着样本量的增加，这种情况会得到有效改善

   

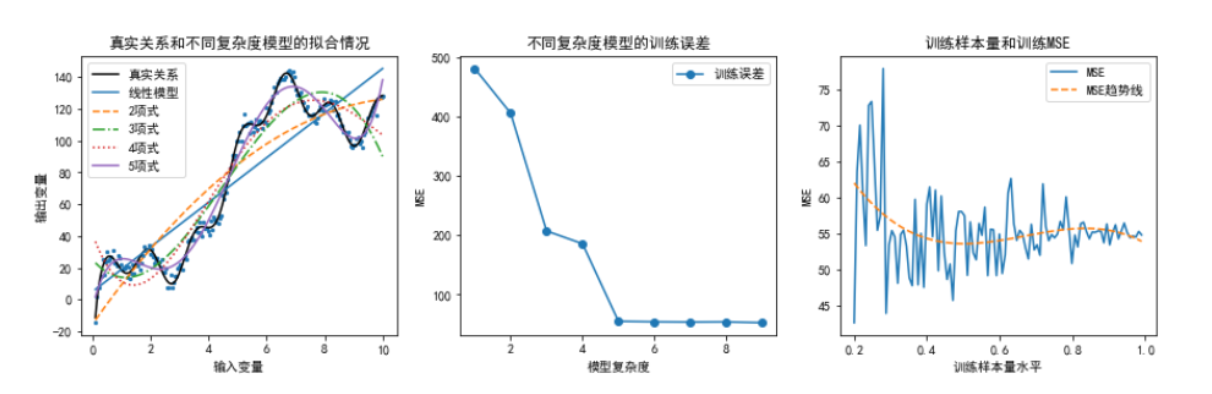
2. 测试误差

   预测建模时，通常只抽取数据集中的部分样本观测组成训练集并训练模型。剩余的样本观测全体称为测试集。评价模型时，将计算模型在测试集上的误差，该误差称为测试误差

数据集的划分策略

数据集划分是将所得数据集划分为训练集和测试集

1. 旁置法

   旁置法将整个数据集随机划分为两个部分，一部分作为训练集（占70%左右），另一部分做测试集

2. 留一法

   用N-1个样本观测作为训练集训练模型，用剩余的一个样本观测作为测试集计算模型的测试误差。该过程需要重复N次，将建立N个模型。

3. K折交叉验证法

   K折交叉验证首先将数据集随机近似等分为不相交的K份，称为K折；然后令其中的K-1份为训练集训练模型，剩余的1份为测试集计算测试误差。该过程需要重复N次，将建立N个模型。