一、数据预测

基本概念

基于已有数据集，归纳出输入变量和输出变量之间的数量关系。根据这种数据关系，可以发现输出变量产生重要影响的输入变量，并且用于对新数据输出变量取值的预测。

• 数据值输出变量的预测称为回归

• 对分类型输出变量的预测称为分类

二、预测建模

预测模型一般以数学形式展开，以便精确刻画和表述输入变量与输入变量取值之间的数量关系。

1. 回归预测模型

   最常见的回归预测模型为

   

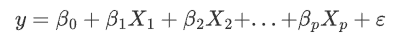
   其中，y为数值型输出变量

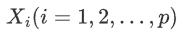   为输入变量

   ε为随机误差项，体现模型之外的其他输入变量对y的影响

2. 分类预测模型

   最常见的分类模型为

   

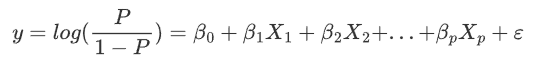
   其中，y为输出变量，只有0，1两个类型，称为二分类预测

   log表示以e为底的自然对数

   P为输出变量（y）取类别值为1的概率

   l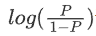记为LogitP，是对P做二元Logistics变换。

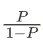   称为优势，即输入变量y=1的概率P(y=1)与y=0的概率P(y=0)之比

   • 广义线性模型

     将上式进行整理，得到

     

预测模型的几何理解

预测建模的出发点，是将数据集中的N个样本观测数据，视为p维实数空间中的N个点。

p的取值与所研究的问题和输入变量的个数及类型有关

预测模型参数估计的基本策略

• 预测建模的参数估计通常以损失函数最小为目标，通常采用有监督学习算法

• 预测建模的参数估计通常借助特定的搜索策略进行

有监督学习算法与损失函数

通常，模型的参数估计以损失函数最小为指导目标。损失函数L是误差e的函数，记为L(e)，与e成正比，用于度量预测模型对数据的拟合误差

• 回归建模中最常见的损失函数为平方损失函数

  

  预测模型对数据全体的拟合误差也称总损失为

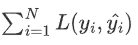
• 分类建模中，常见的损失函数为概率的对数形式，称为交互熵(cross-entropy)

  

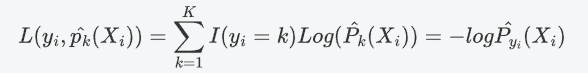
  其中，y_i为样本观测X_i的输出变量（分类型，类别取值为1~k）

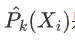  是样本观测X_i的输出变量预测为k类的概率，且满足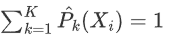

  I(·)称为示性函数，仅有0与1两个函数值，其后面圆括号中为判断条件，条件成立函数值为1，否则为0

  • 二项偏差损失函数（Binomial Deviance Loss Function）

    将y_i的取值固定为0和1，则损失函数可以简化为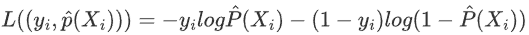，代入整理后的损失函数为

    

  • 指数损失函数（Exponential Loss Function）

    对于y_i取+1与-1的二分类情况，二项偏差损失函数为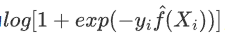，整理后得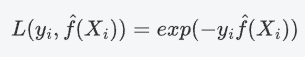

    

  • softmax函数

    对于y_i为K(K>2)分类的情况，损失函数为

    

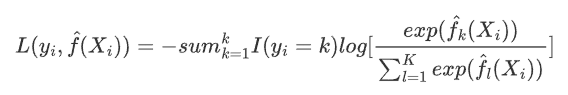
    其中称为softmax函数